Replicating Cornwall's $100k to $30m Strategy [Code Included]
Made famous in "The Big Short", here's how Cornwall Capital turned $100,000 into $30,000,000 through mispriced options.
If you love finance, there’s a good chance that you’ve seen or read: “The Big Short”. And if so, you may be familiar with these two:
In the film, the fund is renamed “Brownfield” as it follows the two’s adventure into getting an ISDA license which would allow them to trade more exotic, institutional products. But well before that, the two had generated extraordinary returns that validated their greater ambitions.
So today, we’ll look at how they did it, why it worked, and multiple examples of how the same strategy is still highly replicable even up to now.
Without further ado, let’s dive right in!
“People hate to think about bad things happening, so they underestimate their likelihood”
The big picture idea of their strategy was to find out where the options market was pricing in a lower probability of an event occurring than their view of the true probability.
To see that clearer, let’s go over one of their early trades:
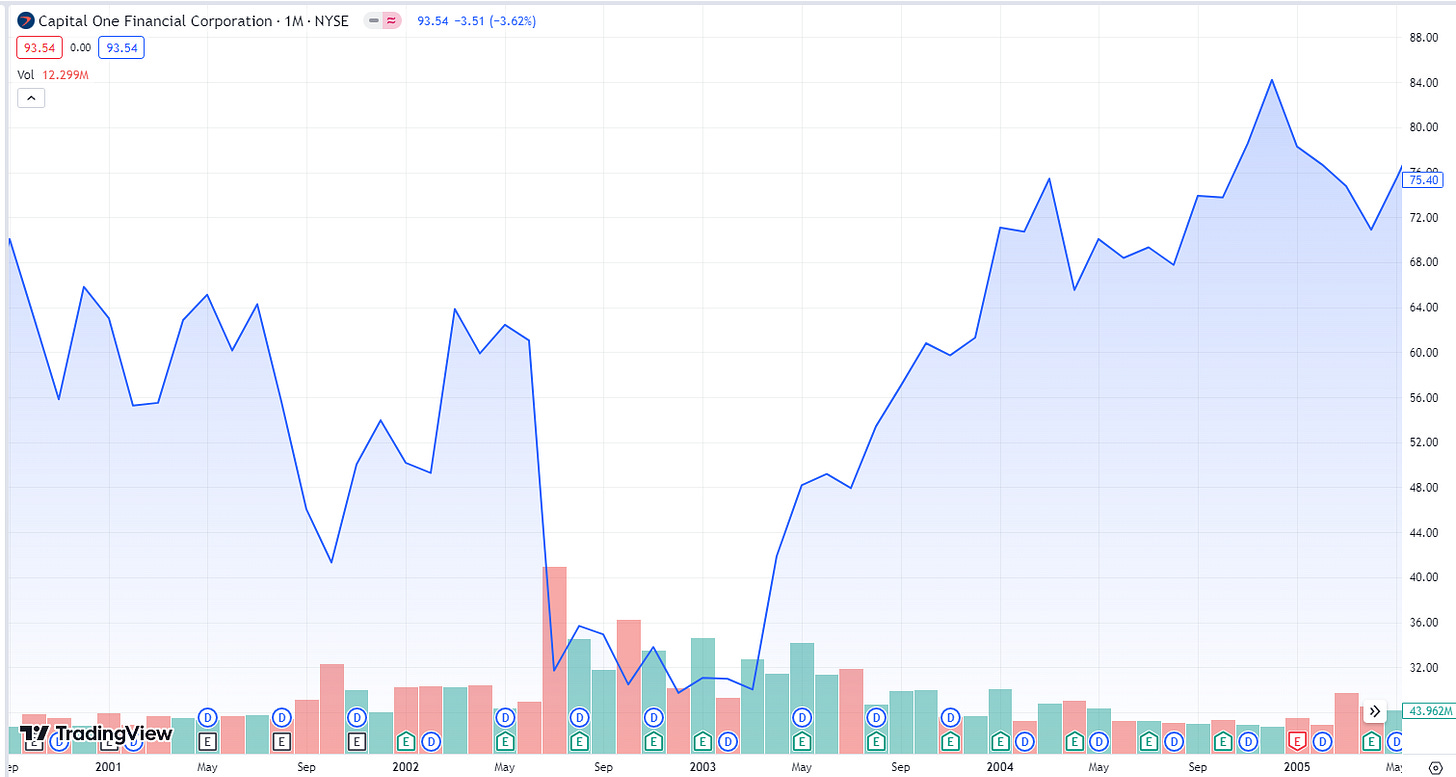
In July 2002, Capital One’s stock was down >40% after management disclosed that regulators were considered them to be under-capitalized. At the same time, several board members (e.g., CFO) were under investigation by the SEC:
Despite the negative market sentiment, Capital One continued to make record profits in the subsequent quarters, even beating earnings estimates.
However, the stock price kept flat and remained range-bound for months. Seeing this, the pair had two conclusions, either:
The reported profits are fraudulent, market sentiment is correct, and the stock should truly be worth $0
or
If the reported financials are true, the overwhelming negative sentiment is vastly wrong and the stock should be worth twice what it’s trading at, $60.
This kind of view implies that option prices should follow a special kind of shape known as a bimodal distribution:
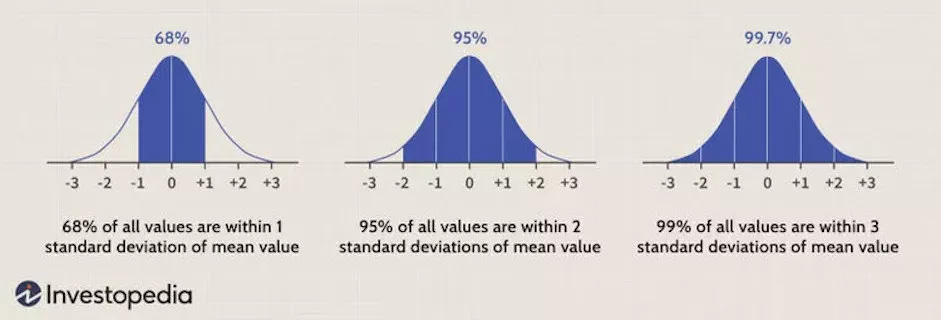
Before understanding how a bimodal distribution works, let’s look at a normal distribution:
When option markets are pricing in a normal distribution, prices are essentially implying that by the expiration date, the underlying stock price will be a value within that bell curve. Strikes that are at the far ends of the curve are priced cheaper, implying a lower probability of them expiring in the money, with those in the center of the curve being more expensive, implying a high probability of expiring in the money.
The two believed that Capital One’s option prices should have been priced as a binomial distribution since they theorized that there was a high probability that the company was worth 0 (left tail edge) and a high probability that it was worth double (right tail edge).
When checking to see what options on Capital One were priced at, they found that the prices did indeed imply a normal distribution. Options that expired in 3 years (LEAPS) that gave the right to buy the stock at $40 ($10 above then current price) traded for only ~$3 per contract. The distribution had a small right tail, implying an extremely low probability of a large positive move in the next 3 years — in stark contrast to the pair’s view.
Realizing the inefficiency, the pair bought 8,000 deep out-of-the-money LEAPS for $26,000 (varying strikes).
In the following months to late 2003, board members and the company were vindicated by the regulatory agencies investigating them, and the stock price had a large up move, going back to its original fair price and beyond:
The initial $26,000 position of 8,000 LEAPS had ballooned to a value of $526,000!
This taste of success gave validation to the strategy of buying cheap LEAPS on incorrect distributions, and they soon repeated it with a European cable television company called United Pan-European, turning $500,000 into $5 million. Then again with a company that delivered oxygen tanks to nursing homes, turning $200,000 into $3 million (source). From then on, it was history.
The pair has since split up, with Jamie continuing to run the fund under H.I.G Capital’s umbrella, at 1.3B AUM. And Charlie now runs a philanthropic fund in Boston.
Why It Worked
The main reasons this worked so well are chiefly the highly asymmetric returns offered by LEAPS, as well as the way options generally price in normal distributions. By executing a view through LEAPS that the market prices as having a low probability, you are offered returns in excess of 1:10. So, when they were wrong (which they were), they lost small, but when they were right — they won big.
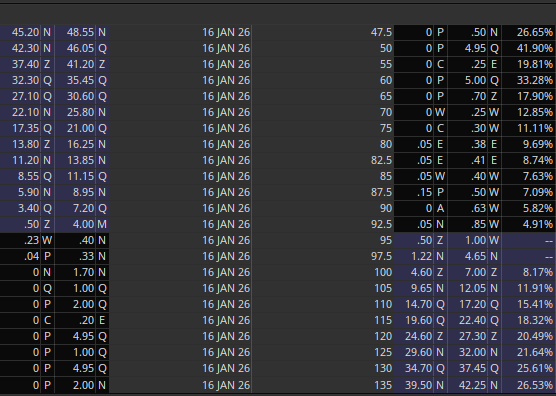
Further, if prices are reflections of the probability of outcomes, then markets are almost always pricing in normal distributions for events. To understand this, let’s visualize a typical options chain:
As pictured, the further away the strike is from the current price, the lower the price of the option gets, thus the lower the probability of the option expiring in the money. In times of special events like earnings, where markets expect higher volatility, the prices are higher due to an increase in implied volatility, but instead of a standard normal distribution, it becomes a fat-tailed distribution:
This prices in extreme moves better, but it still follows a normal distribution shape where there is only one likeliest strike range (center under the curve). In order for options to price a bimodal distribution, prices would have to look like this:
When priced this way, market participants are pricing an equal high probability for there to be a large up move to $103, as well as an equal high probability for a large down move to $98. This almost never happens, so even when options get more expensive to price-in a large move, further out of the money strikes will always be cheaper, enforcing a normal/fat-tailed distribution.
So, now that we’ve seen and understood their strategy, let’s try replicating it today.
Have Markets Gotten Smarter Since?
In order for us to replicate this, we first need a way of knowing what distribution of prices the market expects. There is no closed-form way of doing this, some use the risk-neutral butterfly method, others use the more advanced Breeden and Litzenberger method, but here at The Quant’s Playbook, we make our own.
Instead of trying to estimate an exact X% probability, we will use a probability density function that allows us to answer the question of: “based on option prices, where does the market price-in the highest probability of price at expiration”? The likeliest probabilities will be where investors are paying the most (bids), and the least likely will be where investors are paying the least.
Let’s take a look at a recent real-life example:
Aehr Test Systems (NASDAQ: AEHR) is a company that manufactures test systems for semiconductors and were expected to report earnings on October 5th, 2023. Much like other stocks in the cluster of semiconductors, the stock experienced an enormous rally in 2023, being up more than 100% YTD:
This rally continued uninterrupted, as clearly, the market sentiment on semiconductors and artificial intelligence were extraordinarily positive. As shown in the distribution, taken on October 4th the day before earnings, prices implied a normal distribution, with a higher likelihood to the upside. In other words, options for betting on the stock to go higher were expensive, with options for it to go down being cheaper.
A shrewd investor may see this and build a thesis that: “expectations are very high for this 1977 company, and if earnings aren’t resoundingly positively surprising, the stock price will crater or at least stay flat”. Based on that theory, prices should follow a bimodal distribution, with one peak curve being near the stock price, and another peak curve being further out to the left.
This is different than just buying/selling a put on earnings because with the distribution we are able to quantitatively prove that the thesis has edge. If the distribution implied that a $30 strike price was well within the likely curve, a long put trade would be expensive and have no edge. Conversely if we were sellers, if the distribution implied the $50 strike was at an extreme tail, selling that call strike would have no edge.
Fast forward 1 day and AEHR reported earnings:
It turns out they did get a surprise, but not a resounding one above expectations. As a result, the stock price cratered:
Now, here’s what the new distribution looks like:
As demonstrated, the width of the bell curve shrunk since the volatile event passed, but the curve also moved left, pushing the once center $50 strike far to the right tail, and the $30 strike closer to the probable center — proving the investors’ bi modal thesis correct. This shift in the curve is generally much more dramatic, but this is an options expiration with a few weeks left as opposed to the standard weekly.
But if that doesn’t excite you, here’s a major trade you can actually take now that has a payoff that mirrors those taken by Jamie and Charlie.
The Microsoft-Activision Deal
Long story short, after an initial regulatory blockage, Microsoft is poised to acquire Activision by October 13th for $69 billion at $95 a share. The deal is currently in final review by the UK’s Competition and Markets Authority with a final decision deadline of October 18th. If the deal doesn’t close by this deadline, it is considered dead and Microsoft has to pay Activision ~$4B.
It was originally rejected in both the US and the UK, but after Microsoft agreed to license cloud games to Ubisoft, the deal’s success now seems imminent. At a deal price of $95, the market implies a 99.2% probability of it closing:
There isn’t a single voice in the entire market that thinks this deal won’t go through.
But what if it doesn’t?
What if the CMA (U.K. regulatory agency) puts up another legal challenge and blocks the deal (deal is contingent on approval)? Further, the FTC (Federal Trade Commission) just updated a final challenge to the deal on October 5th. If so, the price of Activision should go back to its pre-merger price of around $60-70 and continue trading. This is unlikely, but it is a non-zero probability, so, there should be a relatively bi-modal distribution. A peak at the merger price, and a peak near the pre-merger price. Let’s check:
This is definitely a wonky normal distribution (short due to cheap prices), but for LEAPS expiring in ~3 years from now, options near the pre-merger strikes (e.g., $70) are priced as having a near 0 probability.
So, step one is confirming that our view is on the tail-end of expectations, but the next step is finding out just how cheap these options are:
As pictured, the market deems this merger so likely, that options expiring in 3 years from now can be picked up for less than $0.50 in both directions. For reference let’s see what options at the same expiration are priced at on, Starbucks, similarly priced at $93.
So, if the deal fails and the share price stays exactly the same as it is now, ATM options on that strip should go from being worth $50 to $1,550, a 31x return. If the deal fails and the price likely drops near its pre-merger price, the deep out of the money options trading for pennies will offer in excess of a 100x return when factoring a surge in implied volatility.
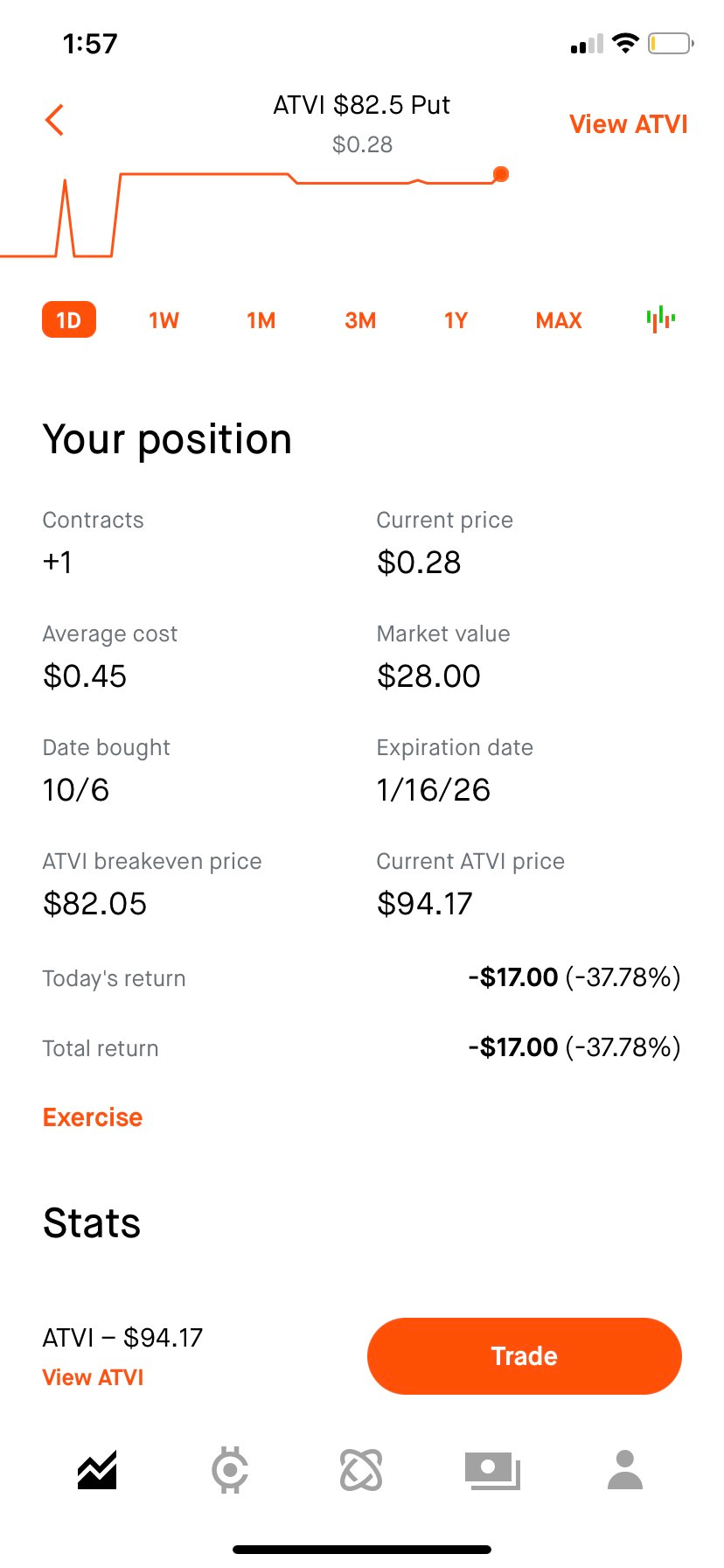
To be sure those prices were actually even tradeable, I bought 1 contract on Robinhood just to see if I’d get filled:
So, these prices are indeed real and tradeable.
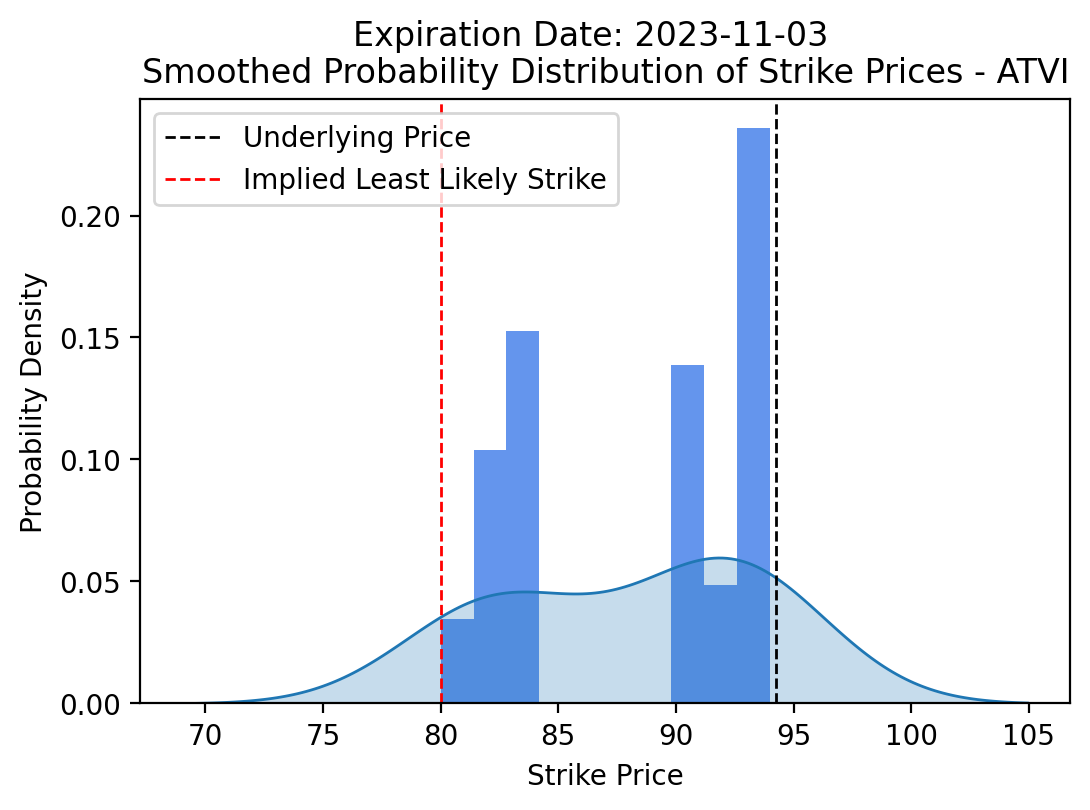
While the 2026 expiration doesn’t price in a failure, the expiration after the deadline (11/03) does quite a good job at it:
Obviously, the odds of the deal being rejected are seemingly extraordinarily low — but in the off chance that the CMA’s decision is that it still violates antitrust laws — this is one hell of a cheap insurance policy. If it goes through, we lose $45 — a tank of gasoline, if it doesn’t — we get back a used car or 2. Make a trade like this 100 times and you’ll end up with a dealership.
I’m considering throwing a bit more on this when the market re-opens, just in case this is the trade to write home about. It probably won’t be, but it’s cheap enough to risk testing.
Final Thoughts
These are the kinds of event-driven trades that made it possible for the 2 to generate such outstanding returns. It might be wrong a good chunk of times, but those few times that it isn’t will allow you to be wrong 20 times over and then some.
I’ve only provided 2 examples of this, but there are thousands of stocks, hundreds with bi-modal catalysts that get created every week (lawsuits, bankruptcies, mergers, spinoffs, etc.). So, if you have the time and effort to build out a strong thesis, and the technology to know where the crowd is (code below), then you can absolutely replicate this strategy and their returns.
Code
You can run the following code straight out of the box, just type in your desired ticker and plots of the distributions of all expiration dates will be generated.
You will need a Polygon.io API key. You can use “QUANTGALORE” for 10% off. I receive no compensation for your use of the code.
https://github.com/quantgalore/option-probability-distribution
Happy trading! 😄

















Hi! I love your posts! :-)
Two questions:
1) How do you mathematically determine the underlying prob. distributions? I am not able to find this in the code? Also, did you compare that to results obtained from Breeden & Litzenberger? Right now, I find it hard to get a feeling for how well your algorithms perform.
2) It would be interesting to see how the change in Implied Vol's in the original trades affected the price. Did you look at the historic prices or do you know where we could ge them from?
Boeing might be a good one to try this on.