Pub-stomping Option Markets with ARIMAX [Code Included]
Holy-grail confirmed. Don't believe me? Deploy it yourself, first-hand.
Pubstomp (v.) - the act of coordinating to execute a well-defined strategy against a randomly-assembled team of players on a public server.
Well, we’ve been doing something very similar; except in this case, we’re not playing video games:
To quickly recap; by using data from all 11 S&P 500 sectors, we trained an ARIMAX model with the goal of predicting the overnight direction of the S&P 500. We theorized that due to the leverage and multiplicative nature of options, the model would only need to be right >50% of the time to generate a long-term profit. In our model analysis stage, we saw figures much better than 50%, so it encouraged us to dive right into production to see how true-to-reality it was.
As demonstrated, it was definitely as real as we hoped for.
So, in what may prove to be a foolish move in retrospect, I am going to release the full code for this so that you may replicate this yourself first-hand.
But before releasing the code, there are a few finer-points that we should touch on.
How Does This Even Work?
To break-down the intricacies of the model, it will help us to capture the story through plots:

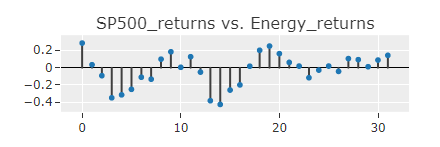
To get a more intuitive understanding, let’s look at the “SP500_returns vs. Energy_returns” plot:
A cross-correlation plot shows the correlation between two different time series at different time lags. For example, in the plot above, the value for 0 on the x-axis represents the correlation of both time series just outright. So, in this case, the returns of the energy sector are correlated with the returns of the S&P 500 by about 30% (0.30).
The concept of time lags come into play after that first value. The value for 1 on the x-axis represents the correlation of 1 time lag. So in this case, it represents the correlation of the energy returns on day 1, compared to the S&P 500’s return on day 2. Which in this case is very close to 0%; this implies that the S&P 500’s next day return is not very much influenced by the prior day’s returns of the Energy sector.
An observation you may have noticed is that in each of the plots, there appears to be a mean-reversion trend across the time lags, before it stabilizes to a constant zero correlation after ~20 days:
So, this is where the power of the model really starts to shine. The AR component of AR.I.MA.X (Auto Regressive), combines all of these correlation values and their mean-reverting nature to help reach a well-rounded prediction. Then, the I component (Integrated) uses those prediction errors to improve itself and better choose the appropriate weights to each sector.
So, now that we’ve taken a peek under the hood of how we’re getting these predictions, let’s look at how we successfully apply it to real-world markets.
From Textbook to Profit
The core logic of capturing this is simple: based on the direction the model expects the market to open, we long/short the asset before close to sell/buy it at the open.
However, the tricky part is determining how we can get the absolute highest leverage possible. To narrow down our search we needed to examine each tradeable S&P 500 product:
3x Leveraged S&P 500 ETFs
SPXL, the Direxion Daily S&P 500 Bull 3X Shares, simply aims to offer 3x the daily returns of the standard S&P 500. So, if SPY increases by 1%, SPXL aims to return 3%.
Despite what you may immediately think, this is actually the most sub-optimal way of capturing this edge, for a few reasons:
While the returns are leveraged, the shares are still priced at ~$97, so if you are starting with a balance of say, $1,000, you will only be able to only purchase about 10 shares per trade.
The options for these products are volatility-adjusted. Since it is known that these products have significantly higher volatility by design, they are quoted with higher implied volatilities. For example, let’s compare the implied volatilites of an ATM call on both SPY and SPXL:
SPY ATM Call Implied Volatility - 10%
SPXL ATM Call Implied Volatility - 30%
This means that we get no additional boost in profit by buying options on this ETF as opposed to options on the standard S&P 500.
No daily expiration options. These products only have weekly expiration options which are inefficient for daily trading since they remain relatively stable due to the preserved time value. We want the 0-DTE options that either loses its value or significantly increases.
So, leveraged ETFs are out.
S&P 500 Futures
The E-Mini S&P 500 futures are both extremely liquid and provide a great deal of leverage. The futures operate on a tick-model where the price only moves in increments of $0.25 (4,000 to 4,000.25). Each tick has a profit value of $12.50, so each $1 move in the future results in a profit or loss of $50 ($12.50 x 4).
On average, the overnight return is around +/- 0.45%, which based on the most recent futures price, implies a $20 price movement (4,607 * .0045). This implies a +/- $1,000 average PnL. This is great, until you see the margin requirements:
The intraday margin would make this a viable choice if we were trading during the day, but this is specifically an overnight strategy, so that means we would have to post upwards of $12,000 of capital with an expectation of a $1,000 profit or loss.
But are the options any better?
The options suffer the same cost-prohibitiveness since the strikes are only quoted in increments of $5:
Additionally, since the futures are not a leveraged product — if the S&P 500 rises by 1%, the returns of an ATM futures call will be virtually identical to the returns of an ATM call on SPY, since both products represent the same underlying index.
So, E-Mini futures are also out.
SPY ETF Options
This brings us back to our original strategy of using basic calls and options on SPY.
Not only are 0-DTE options available, but the costs can be extremely low, increasing accessibility to all traders; large and small. In recent times (relatively low volatility), the cost for an ATM option expiring on the next day is around $87-130. Since we’re just buying the options, this is the total cost and we don’t incur losses greater than that premium.
We still get the multiplicative nature of derivative contracts, and liquidity isn’t even a fore-thought as this is arguably the most liquid option chain in the entire investing universe.
So, SPY options are in!
The Strategy
So, now that we have what we believe to be the most optimal instrument, we can now iron out the most optimal way to use the instruments.
Keep reading with a 7-day free trial
Subscribe to The Quant's Playbook to keep reading this post and get 7 days of free access to the full post archives.