A Junior Quant's Guide to +EV Options Trading [Code Included]

It's a bird, it's a plane... it's a mathematically guaranteed profit!

Positive expected value (adj.); A condition in which the average outcome of an event yields a net gain over time.

You’ve heard about it, you’ve read about it, you need it, but how do you actually get it?

It’s an elusive question — ask it to 100 different traders and you’ll get 100 different answers. So today, we’re going to set the record straight.

We’ll be taking a practical deep dive into how a real-world quantitative trading operation can evaluate options and find +EV trades. At the end, we’ll also provide you with some tools that will allow you to play with some data and find these opportunities yourself.

So, without further ado, let’s get right into it:

Want EV? Get a View. Seriously, Get a View.

As a quant, the concept of positive EV is one you end up basing your entire life on:

Scenario: “I’m running a quick 10-minute errand, if I skip the $2 parking meter fee, I’ll save $2 — if I get caught, I’ll be fined $45. If there is a 10% chance of being caught and fined, will skipping the fee be an advantageous decision?”

Theoretical EV = (win_rate * gain) + (loss_rate * loss)

Theoretical EV = (.90* 2) + (.10* -45)

Theoretical EV = $-2.70

So, before taking any risk at all, we can know with near certainty that not paying the fee would be a terrible decision (by the way, this was a real scenario we calculated in a real life parking lot — maybe we’re a little too serious about this…).

Moving on, we can naturally extend this to option markets.

We know that implied volatility represents the 68% confidence interval for that security’s realized move. In other words, 68% of the time, realized volatility will be less than or equal to what’s implied — 32% of the time, it’ll be greater.

Now, let’s say we have a model that accurately predicts returns 51% of the time. Extreme amounts of money are made when you accurately predict the direction and get a larger-than-implied move, so let’s get a rough probability of this scenario taking place:

Theo Probability = (proba_of_rv_greater_than_iv * proba_of_accurate_direction)

Theo Probability = (.32 * .51)

Theo Probability = ~16%

So, on any given trade (assuming no edge), there’s about a 16% probability that we’ll accurately predict the direction and have the move be greater than implied. This means that we need at least a 6x return on the winning trades to break-even.

We can isolate the options that will have this payoff by simply simulating the future option price based on a given move:

1. We take the current price and implied volatility of an out-of-the-money option

2. We use an options pricing model (e.g., Black-Scholes) to get the price of the option if the stock price moves +/- the implied move.

   1. For instance, say we’re looking at the 105 strike call. If the stock price is currently $100 and the implied move is 10% in a day, we price the 105 call using a stock price of 110.01 to see what it would be worth.

      1. We make sure to also decrease the time to expiration of this theoretical option by 1-day.

3. We take the future theoretical price, subtract it from the price it’s currently trading at and use that as our theoretical PnL.

In theory, if we put together a large portfolio of options that all had a theoretical PnL of >6x the initial price, we would have a mathematical “guarantee” of profits, even at a win rate of ~16%.

We’ve got all the data in the world, so all we’d need to do is run through each weekly options chain, see what each would be worth if a greater than implied move occurred in the next day, then if it meets our PnL criteria, we add it to our portfolio.

So, let’s do it:

1. For a given day, we pull the options chain for a given stock.

2. We calculate the next-day future price as whatever the implied move is (IV / sqrt(252), plus $0.01.

   1. So, if the stock price is $100 and the implied move is 10%, we price the available options as if the spot price tomorrow is $110.01/$89.99.

   2. We use this because it’s a reasonable estimate of what the stock price will be if RV >IV.

      1. Obviously, there will be options that return much higher than 6x if the realized move is 10x higher than implied, but realistically, we should model what happens if the realized move is just outside of implied.

      2. Our core assumption is that there is a 32% chance of RV being greater than IV, that assumption starts to break down if we’re modeling the chances of RV being n times greater than IV.

3. If there are options that provide our desired theoretical PnL (~5.25x), we add it to the portfolio at near market close, then sell the portfolio at the next day’s market close.

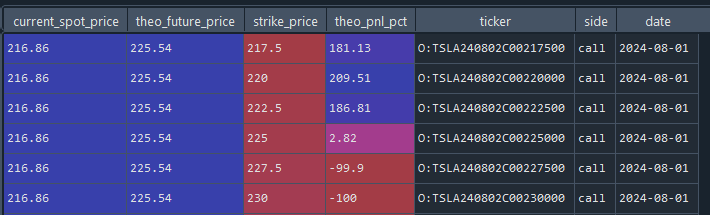
Here’s an example of the output we’d see for a call strip: